Ультраэллиптические интегралы и функции

Квадратуры вида: 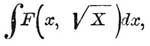, где Χ есть целый полином степени выше четвертой относительно x, a F — какая-либо рациональная функция от x и √x называются У. или гиперэллиптическими интегралами.

Теорией У. интегралов занимались Абель, Якоби, Гёпель, Розенгайн, Эрмит, Вейерштрассе, Прим, Нейман, Клебш и Гордан, Г. Вебер, Томэ, Брио, Кенигсбергер и др.; у нас, в России, К. А. Поссе, П. М. Покровский, М. А. Тихомандрицкий и др.

Если Χ есть полином 5-й-или 6-й степени, то интегралы называются У. первого класса. С помощью подстановки:

x = (a + by)/(c + fy)

всегда возможно интеграл с полиномом Χ шестой степени относительно x привести к интегралу с полиномом Y пятой степени относительно у.

Те У. интегралы первого класса, которые могут быть приведены к виду:

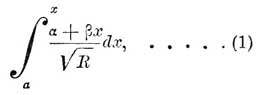
где R = x(1 — x)(1 — χ²x)(1 — λ²x)(1 — μ²x), а величины a, α, β, χ, λ, μ — постоянные, называются ультраэллиптическими интегралами первого класса и первого рода. Они конечны для всех значений переменной х.

Если интеграл 1-го класса приводится к виду

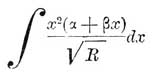
то он называется ультраэллиптическим интегралом второго рода. Он обращается в бесконечность алгебраически при х = ∞. Интеграл, приводящийся к виду:

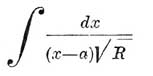
называется ультраэллиптическим интегралом третьего рода; он обращается в бесконечность логарифмически при x=a.

Начало теории ультраэллиптических интегралов было положено в 30-х годах прошлого XIX стол. знаменитою теоремою Абеля о сложении интегралов алгебраических функций. Из этой теоремы между прочим следует, что если имеем систему уравнений

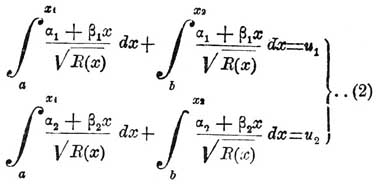
то х₁ и x₂, как функции от u₁ и и₂ суть корни квадратного уравнения:

Nx² + mx + L = 0,

в котором N, М и L суть однозначные функции от и₁ и и₂.

Якоби показал, что L, M и N суть однозначные функции с четырьмя системами периодов, т. е. что они остаются без изменения, если одновременно заменим и₁ и и₂ через

и_{1 +} n₁A₁ + n₂B₁ + n₃C₁ + n₄D₁

и_{2 +} n₁A₂ + n₂B₂ + n₃C₂ + n₄D₂

где п₁, п₂, п₃, п₄ суть какие-либо целые числа, a A₁, В₁,С₁, D₁ и А₂, В₂, С₂, D₂ периоды двух интегралов в равенствах (2).

Требовалось определить те функции от и₁ и и₂, которые выражали бы х₁ и x₂ и соответствующие им значения √R(x₁) и √R(x₂), удовлетворяющие уравнениям (2).

Эта задача была решена почти одновременно Гёпелем и Розенгайном, которые показали, что для решения ее надо ввести особые функции от двух переменных, названный функциями Θ (тета) от двух аргументов; начало теории таких функций положил Риман.

Функция Θ от двух аргументов и₁ и и₂ выражается двойным бесконечным рядом.

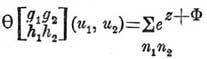
где:

z = 2(n₁ + g₁/2)(u₁ +[h₁/2]πi) + 2(n₂ + g₂/2)(u₂ + [h₂/2]πi)

Ф = (n₁ + g₁/2)²τ₁₁ + 2(n₁ + g₁/2)(n₂ + g₂/2)τ₁₂ + (n₂ + g₂/2)²τ₂₂

и где, в сумме, целые числа п₁ имеют всевозможные величины от —∞ до +∞ и целые числа п₂ имеют всевозможные величины от —∞ до +∞. Величины g₁, g₂, h₁, h₃, τ₁₁, τ₁₂, τ₂₂ суть постоянные.

Совокупность постоянных g₁, g₂, h₁, h₂ называется характеристикою функций Θ. При исследовании свойств этих функций оказывается, что существует только 16 различных функций Θ, а именно соответствующих характеристикам:

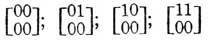
и т. д., при которых g₁, g₂, h₁, h₂ суть либо нули, либо единицы.

Функция Θ с характеристикой 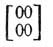обозначается просто через Θ(u₁u₂).

По изучении свойств этих функций Θ оказалось, что х₁ и x₂, а также √R(x₁) и √R(x₂) выражаются рационально в функциях Θ от двух аргументов и₁ и u₂.

Для знакомства с теориею ультраэллиптических интегралов и функций Θ от двух аргументов нужно обратиться к статьям и сочинениям вышеупомянутых ученых.

Д. Б.