симметрия молекул

СИММЕТРИЯ МОЛЕКУЛ

совокупность операций симметрии, применение которых переводит молекулу в физически тождеств. объект (саму в себя). Операциями С. м. считаются преобразования пространства и времени, а также перестановки тождеств. частиц. Выполнение операций С. м. оставляют без изменений уравнения, выражающие физ. законы; иными словами, эти уравнения инвариантны относительно операций симметрии. При последоват. выполнении неск. операций симметрии инвариантность сохраняется на каждом шаге; операции симметрии образуют в мат. смысле группу. В частности, физ. законы должны быть сформулированы так, чтобы они отражали постулируемые на основании опытных данных однородность и изотропность пространства и неразличимость тождеств. частиц.

Операции С. м. В отсутствие внеш. сил произвольные трансляции (линейные движения в пространстве без вращения) и повороты молекулы как целого не меняют ее свойств и не меняют вид уравнений, определяющих ее поведение; это находит отражение в сохранении полного импульса молекулы и ее момента импульса. Операциями симметрии молекулы как пространств. тела, совмещающегося при таких операциях со своей исходной конфигурацией, являются: 1) повороты вокруг оси симметрии на угол 2πk/n (обозначаются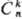), где k и n-целые числа (k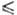и); эта ось наз. осью вращения n-го порядка; 2) отражения в плоскости (обозначаются σ); 3) зеркальные повороты (обозначаются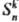), которые сводятся к поворотам C^k_n и последующему отражению в плоскости σ_n, перпендикулярной оси вращения; 4) инверсия относительно начала системы координат, когда все координаты x, у и z переходят в — x, — у и — z соотв. (обозначается i или E*). К. числу операций симметрии относят и тождеств. (тривиальную) операцию, оставляющую пространств. тело без изменений (обозначается E).

В рамках классич. представлений о строении молекул свойства симметрии рассматривают прежде всего для равновесных конфигураций ядер. Например, линейная молекула CO₂ переходит сама в себя при любых поворотах вокруг ее оси и при отражении в плоскости, перпендикулярной этой оси и проходящей через атом С; молекула CH₄ имеет симметрию правильного тетраэдра и т. п. В квантовой механике в наиб. общем смысле С. м. определяется той группой преобразований, по отношению к которым инвариантно уравнение Шрёдингера, или в релятивистской квантовой теории-уравнение Дирака либо уравнение Брейта — Паули (см. спин) и т. п. Каждая группа преобразований носит назв. группы соответствующего уравнения (напр., группы уравнения Шрёдингера). Эти группы включают: а) произвольные трансляции и повороты своб. молекулы как целого; б) инверсию координат всех частиц относительно центра масс молекулы; в) обращение времени, эквивалентное обращению знака у всех операторов импульса и момента импульса; г) перестановки тождеств. частиц, напр. электронов; д) все операции точечной группы симметрии, при которых совмещается сама с собой ядерная конфигурация молекулы. Осн. роль играют операции, указанные в пунктах г и д, а также инверсия, поскольку именно они специфичны для каждой конкретной молекулы.

Точечные группы С. м. включают повороты, отражения, зеркальные повороты и инверсию относительно начала системы координат. Каждая из точечных групп включает и тривиальную (единичную) операцию, отвечающую отсутствию преобразования пространства. Для каждой точечной группы симметрии есть хотя бы одна неподвижная при всех операциях этой группы точка, в качестве которой у молекул выступает центр масс.

При рассмотрении С. м. для точечных групп обычно используют обозначения Шёнфлиса . Простейшие точечные группы включают всего лишь единичную операцию и один нетривиальный элемент симметрии; ими являются: C₂-группа, содержащая вращение вокруг оси второго порядка; C_s- группа, содержащая отражение в плоскости; C_i- группа, содержащая инверсию. Более сложными являются группы: C_n, включающие повороты вокруг оси n-го порядка; C_nu (в т. ч. C_,u), возникающие при расширении групп C_n операциями отражения σ_u в n плоскостях, проходящих через ось симметрии C_n (группы симметрии правильных n-угольных пирамид); C_nh, включающие операции групп C_п и отражение σ_h в плоскости, ортогональной оси симметрии C_n; группы S_n(n = 2k), состоящие из зеркальных поворотов S_n на угол (π/n) l, где l = 1, 2,...n; группы D_n, включающие все повороты, которые совмещают правильную n-угольную призму саму с собой; D_nh-группы симметрии правильной n-угольной призмы, т. е. расширение групп D_n соответствующими операциями отражения; группы D_nd-группы симметрии правильных n-угольных антипризм; T_dt O_h и I_h-группы симметрии правильных тетраэдра,-октаэдра и икосаэдра соответственно. Эти точечные группы наиб. часто встречаются при анализе С. м.

При рассмотрении кристаллохим. задач более распространена международная символика точечных групп (или символика Германа-Могена). В ней плоскость симметрии обозначается буквой m, ось симметрии-цифрой, указывающей ее порядок; зеркально-поворотная ось-соответствующей цифрой с чертой над ней, причем в качестве операции зеркального поворота рассматривается поворот с послед. инверсией (а не отражением в перпендикулярной плоскости, как то было выше). Кроме того, перпендикулярность оси вращения и плоскости симметрии отмечается символом дроби "/". Так, группа (4/m)mm, обозначение которой обычно упрощают до 4/mmm, включает повороты вокруг оси четвертого порядка С₄, отражения σ_h в плоскости и отражения σ_u и σ'_u в двух неэквивалентных плоскостях, т. е. это группа D_4h в обозначениях Шёнфлиса . Все остальные операции, входящие в группу, определяются как те или иные произведения указанных операций.

Группы перестановок для системы N тождеств. частиц обычно обозначают S_N. Если имеются две подсистемы из N₁ и N₂ тождеств. частиц (напр., в NH₃ подсистемы протонов и электронов), полной группой перестановок для всей системы будет группа S_N1∙S_N2, наз. прямым произведением групп и включающая все парные комбинации операций С. м. для первой и для второй подсистем.

Для молекулы, включающей N тождеств. частиц, возможны N! перестановок частиц, из которых выделяют N(N — 1)/2 простейших, т. наз. транспозиций — перестановок индексов двух частиц; все остальные перестановки получаются при последоват. применении неск. транспозиций. Волновая функция молекулы при транспозициях, включающих помимо пространств. координат частиц их спиновые индексы, либо меняет знак, если спин частиц полуцелый (т. е. если части-цы фермионы), либо остается без изменений, если спин частиц целый (т. е. если частицы бозоны). Говорят, что для системы тождеств. фермионов волновая функция антисимметрична относительно перестановок (преобразуется по антисимметричному представлению), волновая функция системы тождеств. бозонов полносимметрична относительно перестановок (преобразуется по полносимметричному представлению, см. ниже).

В качестве примера рассмотрим симметрию молекулы ¹²C₃H₆. В ней имеются три подсистемы тождеств. частиц: ядра углерода ¹²С (с ядерным спином I = 0), 6 протонов (I = 1/2) и 24 электрона (со спином s — 1/2). Следовательно, волновая функция молекулы полносимметрична относительно перестановок индексов ядер ¹²С и антисимметрична относительно перестановок индексов как протонов, так и электронов. С др. стороны, у ¹²C₃D₆ волновая функция полносимметрична относительно перестановок индексов дейтронов (I = 1).

При рассмотрении симметрии ядерной конфигурации и классификации колебательно-вращат. состояний молекулы важна перестановочно-инверсионная группа, включающая наряду с операциями перестановок тождеств. частиц также инверсию и все произведения перестановок и инверсии. Др. словами, перестановочно-инверсионная труппа представляет прямое произведение групп S_N и С_i. Порядок этой группы, т. е. число содержащихся в ней элементов, м. б, очень большим. Так, для циклопропана при рассмотрении только лишь подсистемы ядер порядок перестановочно-инверсионной группы равен: (порядок группы C_i, равный 2) x (порядок группы S₃ для ядер ¹²С, равный 3!) x (порядок группы S₆ для протонов, равный 6!), т. е. перестановочно-инверсионная группа включает 2 x 6 x 720 = 8640 операций. Точечные группы С. м. изоморфны подгруппам соответствующих перестановочно-инверсионных групп, т. е. между операциями симметрии точечных групп и этих подгрупп существует взаимно однозначное соответствие.

Группы уравнения Шрёдингера. При выполнении операций этих групп оператор Гамильтона H не меняется. Отсюда следует, что волновая функция Y при выполнении любой операции P_k из такой группы переходит в волновую функцию P_kY, которая также является решением уравнения Шрёдингера. Следовательно, если некоторая группа G включает конечное число операций P_k (k = 1, 2,..., К), то все функции P_kY, наряду с Y, являются решением исходного уравнения. Для стационарного состояния мол. системы все эти функции будут соответствовать одной и той же энергии. Если среди всех функций P_kY есть несколько линейно независимых (напр., Ф₁ = Y и Ф₂ = P_kY), а все остальные функции Р_lY (l. k) линейно выражаются через них, то для описания состояний системы достаточно знать, как преобразуются при операциях симметрии именно эти независимые функции. Совокупность преобразований при операциях симметрии линейно независимых волновых функций Ф_i (i = 1, 2,..., m) из общего множества К функций P_kY наз. представлением группы. Для того чтобы говорить о преобразованиях волновой функции Y при операциях С. м., нужно, по существу, сказать о том, как при этом она переходит в линейные комбинации функций Y_i; иными словами, по какому представлению группы функция Y преобразуется или к какому типу симметрии она относится. Среди всех возможных представлений каждой конечной группы всегда можно выделить такие, к которым сводятся все остальные представления; они наз. неприводимыми представлениями. Все волновые функции, являющиеся решениями уравнения Шрёдингера, преобразуются по тому или иному неприводимому представлению группы симметрии этого уравнения.

Симметрия поверхностей потенциальной энергии (ППЭ).

При введении приближений, позволяющих упростить решение уравнения Шрёдингера, часто появляются дополнит. операции С.м., которых в исходной, точной постановке задачи не существует. Так, широко распространено адиабатическое приближение, согласно которому электроны предполагаются движущимися в фиксир. поле ядер, создаваемом их мгновенной конфигурацией, тогда как ядра движутся в усредненном по всем конфигурациям электронов потенц. поле, совпадающем для стационарной задачи с электронной энергией. Электронная волновая функция Y_i(r, R) так же, как и электронная энергия E_i(R), параметрически зависит от ядерных переменных R (r-обозначение пространств. переменных электронов), что позволяет учесть влияние С.м. по отношению, напр., к перестановкам ядер, на свойства функций Y_i и E_i.

Если выбрать к.-л. конфигурацию ядер и отвечающую ей электронную энергию, то при всех операциях перестановочно-инверсионной группы, т. е. при всех перестановках тождеств. ядер, напр. протонов в циклопропане, и при инверсии эта энергия остается без изменений, т. е. ППЭ молекулы симметрична относительно таких операции. Это утверждение имеет важные следствия. Действительно, пусть ядерная конфигурация молекулы отвечает некоторой точечной группе, напр. D_3h. Каждая из операций симметрии меняет местами (переставляет) тождеств. ядра; это означает, что операции точечной группы эквивалентны некоторому подмножеству операций соответствующей группы перестановок, т. е. точечная группа является подгруппой группы перестановок уравнения Шредингера. Т. к. при операциях точечной группы С. м. электронная энергия не меняется, любая точка на ППЭ (в т. ч. и не отвечающая симметричной конфигурации) переходит, вообще говоря, в др. точку на ППЭ с той же энергией. В частности, если исходная точка отвечала минимуму (локальному или глобальному), то и вновь полученная точка также будет отвечать минимуму. Следовательно, операции симметрии "размножают" экстремальные и др. особые точки на ППЭ, за исключением тех случаев, когда они переводят ядерную конфигурацию саму в себя, т. е. когда точка на ППЭ при операциях С. м. остается неподвижной. Это означает, что ППЭ в целом всегда обладает максимально допустимой для данной системы ядер симметрией. Так, для ППЭ N₂H₄ максимально допустимая симметрия D_4h (линейные конфигурации не учитываем, поскольку отвечающие им операции симметрии приводят в осн. лишь к поворотам системы ядер как целого). В то же время равновесная конфигурация ядер имеет симметрию точечной группы C₂.

При этом рассмотрении были учтены лишь операции симметрии точечных групп, допустимых для конкретных молекул. В более общем случае необходимо использовать операции симметрии перестановочно-инверсионной группы либо тех ее подгрупп, которые включают т. наз. физически допустимые операции, не приводящие, напр., к изменению последовательности хим. связей в молекуле.

Др. важное следствие состоит в том, что точки на ППЭ, отвечающие симметричным ядерным конфигурациям, являются экстремальными по отношению к несимметричным смещениям ядер. Так, если для молекулы H₂O с равными межъядерными расстояниями O—H, имеющей симметрию ядерной конфигурации С_2u, произвести смещение ядер О и H без изменения симметрии, то при операциях точечной группы эта конфигурация останется без изменений. Если же смещение несимметрично, напр. одна связь О—H стала длиннее, другая короче, то при операциях симметрии ядерная конфигурация переходит в другую, но с той же электронной энергией. Уменьшая последовательно смещение ядер до нуля и каждый раз выполняя одну и ту же операцию симметрии, получим некоторую кривую, соединяющую исходные точки, на которой лежит и симметричная конфигурация. Очевидно, что в точке, отвечающей симметричной конфигурации, производная вдоль этой кривой будет равна нулю, что служит подтверждением высказанного утверждения.

При наличии вырождения ППЭ, которое обусловлено С. м. и устраняется при несимметричных искажениях геом. конфигурации ядер, утверждение об экстремальности симметричных конфигураций сохраняется, однако при этом отдельные несимметричные конфигурации, "размноженные" операциями симметрии, будут, вообще говоря, расположены ниже по энергии, чем исходная симметричная, для которой возможно вырождение. Эта ситуация составляет основу Яна-Тел-лера эффектов.

Таким образом, симметричные конфигурации ядер играют определяющую роль в описании топологии ППЭ молекул. Для H₂O, напр., возможны симметричные конфигурации ядер, преобразующиеся в себя операциями точечной группы C_2u, и конфигурации симметрии D_,h. Группа C_2u является подгруппой D_,h, а остальные операции группы D_,h представляют собой всевозможные повороты вокруг оси C_∞ и инверсию-отражение в плоскости, перпендикулярной этой оси, с послед. поворотом на угол π вокруг C_∞. Повороты приводят к вращениям всех других (нелинейных) конфигураций H₂O, а инверсия дополнительно определяет т. наз. четность вращат. состояния, которая связана с тем, меняет или не меняет знак при инверсии вращат. волновая функция молекулы.

В общем случае при вращениях молекулы как целого каждой конфигурации ядер отвечает эллипсоид инерции, определяющий эти вращения и обладающий симметрией точечной группы D_2h (либо более высокой, если две или все три оси эллипсоида равны друг другу). Поэтому вращат. состояния молекул можно классифицировать по неприводимым представлениям группы D_2h.

Симметрия равновесной конфигурации молекулы. Как правило, в хим. приложениях рассматривают равновесные конфигурации молекул. С ними соотносят все закономерности строения молекул и на их основе проводят большинство корреляций свойств молекул со строением. Очень часто, особенно у малых молекул, содержащих атомы элементов 2-го и 3-го периодов периодич. системы, равновесная конфигурация молекулы в основном электронном состоянии, отвечающая минимуму на ППЭ, является симметричной. Есть и др. симметричные ядерные конфигурации, но они отвечают не минимуму, а, напр., максимуму на ППЭ. Так, у молекулы NH₃ возможна, помимо симметрии C_3u, симметрия D_3h, когда все 4 ядра лежат в одной плоскости. Однако такой конфигурации отвечает локальный максимум на сечении ППЭ основного состояния; отражение в этой плоскости переводит одну равновесную конфигурацию NH₃ в другую, ей эквивалентную. Переход же молекулы из одного минимума на ППЭ в другой в этом случае носит назв. пирамидальной инверсии.

При электронном возбуждении симметрия равновесной конфигурации может меняться. У аммиака, напр., равновесная конфигурация ряда возбужденных состояний имеет симметрию D_3h; молекула этилена в основном состоянии плоская, с симметрией D_2h, при возбуждении переходит в состояние с равновесной конфигурацией симметрии D_2d и т. д. Аналогичные изменения симметрии равновесной конфигурации проявляются и при ионизации молекул.

Равновесные конфигурации молекул могут менять симметрию при переходе вещества из газовой фазы в конденсированную. Так, в газовой фазе фенильные кольца бифенила повернуты друг относительно друга на угол, примерно равный 40°, и молекула имеет симметрию D₂, тогда как в кристалле ее равновесная конфигурация плоская, симметрии D_2h. У молекулы нафталина с симметрией равновесной конфигурации D_2h в газовой фазе при переходе в кристалл симметрия понижается до C_2h. И хотя при этом изменения длин связей (межъядерных расстоянии между соседними центрами) невелики, все же переход от одного типа С.м. к другому четко проявляется, напр. в мол. спектрах.

Следует отметить, что при изотопич. замещении атомов в молекуле ППЭ практически не меняется, в силу чего не меняется и симметрия равновесной конфигурации.

Локальная симметрия отдельных фрагментов молекулы, как и С. м. в целом, определяется теми операциями точечной группы, которые переводят этот фрагмент в себя. Например, в молекуле метана (группа T_d) операции симметрии, оставляющие на месте заданный атом водорода, образуют подгруппу С_3u группы тетраэдра, так что локальная симметрия определяется именно этой подгруппой. Задание локальной симметрии особенно полезно, если можно выделить фрагмент молекулы без учета его окружения, а влияние окружения рассматривать как малое возмущение. Так, в толуоле метильный фрагмент имеет ариближенную локальную симметрию С_3u, тогда как реальная симметрия этого фрагмента-C_s. Указание локальной (точной или приближенной) симметрии позволяет, в частности, дать более детальную информацию о молекуле. Для В₂O₃, напр., указание лишь группы симметрии C_2u не позволяет судить о том, линеен или изогнут фрагмент О—В—О (локальная симметрия соотв. C_,u или С_2u), тогда как запись С_2u [В:С_2u] говорит о том, что угол О—В—О отличается от 180°.

Симметрия нежестких молекул. У молекул, имеющих два или более эквивалентных минимума на ППЭ, разделенных невысокими барьерами, возможен с большой вероятностью относительно быстрый переход из одного минимума в другой. Операции симметрии, переводящие одну конфигурацию в эквивалентную ей другую, входят в перестановочно-инверсионную группу С. м. Эти операции, как правило, можно связать с теми или иными поворотами, отражениями и инверсией; операции, переводящие исходную конфигурацию нежесткой молекулы в энергетически ей эквивалентную, носят назв. изодинамич. операций. Так, для NH₃ существует изодинамич. операция σ_h — отражение в плоскости, проходящей через центр масс молекулы перпендикулярно оси 3-го порядка. Если исходную группу С_3u дополнить операцией σ_h и всеми теми, которые получаются при последо-ват. выполнении операции σ_h и к.-л. операции из группы С_3u, получится группа D_3h. Именно эта группа, являющаяся прямым произведением групп С_3u и C_s и изоморфная перестановочно-инверсионной группе C_i x S₃, представляет группу симметрии NH₃ как нежесткой молекулы. Для молекулы C₂H₆ возможны повороты вокруг оси C₃ не всей молекулы в целом, а одной метальной группы относительно другой. Изодинамич. операции (вместе с тождеств. операцией) образуют группу. В результате полная группа С. м. будет состоять из всех произведений операций точечной группы на операции изодинамич. группы, т. е. является произведением этих двух групп. Для молекулы CH₃BF₂ с плоской координацией атомов у атома В и тетраэдричес-кой у атома С точечной группой симметрии является C_s или С₁, изодинамич. группа, напр. для конфигурации с симметрией C_s, включает повороты CH₃ вокруг оси 3-го порядка, соединяющей атомы С и В, и повороты BF₂ вокруг оси 2-го порядка, совпадающей с осью 3-го порядка. Поэтому изодинамич. группой в этом случае будет I = C₃ x C₂, а полной группой S = (С₃ x С₂) x C_s. Она является подгруппой перестановочно-инверсионной группы для молекулы CH₃ BF₂.

Таким образом, для нежестких молекул, у которых допустимы изо-энергетич. переходы из одной конфигурации в другую, группы симметрии являются более сложными по сравнению с точечными группами, отвечающими обычным операциям преобразования пространства; в общем случае они, однако, изоморфны подгруппам перестановочно-инверсионной группы.

Орбитальная симметрия. Симметрия ядерной конфигурации влечет за собой вполне определенное поведение электронной волновой функции, а именно: при операциях симметрии она преобразуется по одному из неприводимых представлений группы С. м. В общем случае при представлении многоэлектронной волновой функции через произведения одноэлектронных функций (орбиталей) утверждать что-либо о преобразованиях орбиталей при операциях симметрии достаточно сложно. Однако в ряде сравнительно простых подходов такие заключения м. б. сформулированы. Так, если для молекулы с замкнутой оболочкой волновая функция, записанная в приближении Хартри — Фока, аппроксимирует невырожденное электронное состояние, мол. орбитали преобразуются каждая по к.-л. из неприводимых представлений той же группы симметрии, т. е. по тому или иному типу С. м. Из таких мол. орбиталей можно составлять детерминанты Слейтера или конфигурац. функции состояния заданного типа симметрии для аппроксимации электронных волновых функций молекулы именно этого типа симметрии (см. конфигурационного взаимодействия метод).

Симметрия молекул относительно обращения времени приводит к детального равновесия принципу, который играет важную роль при анализе разл. каналов осуществления хим. реакции. Этот принцип утверждает, что вероятность перехода между квантовыми состояниями для обратного процесса f₁ : i₁ с параметрами состояний f₁ и i₁, отвечающего обращенному времени, равна вероятности перехода для прямого процесса i : f. Здесь индексы с цифрой 1 обозначают волновые функции состояний с заменой времени t на — t (подробнее см. в ст. динамика элементарного акта хим. реакций).

Проявления симметрии. Наличие симметрии ядерной конфигурации отчетливо проявляется во всех свойствах молекулы. Если уравнение Шрёдингера имеет группу операций симметрии, не меняющуюся с течением времени, то волновая функция, являющаяся решением этого уравнения, сохраняет свой тип симметрия с течением времени. Для того чтобы тип симметрии волновой функции изменился, необходимо воздействие возмущения, устраняющего исходную С. м.

Любое воздействие на атом или молекулу в квантовой механике представляется оператором, который зависит от переменных частиц, составляющих такую систему, и, следовательно, также может обладать определенной симметрией. Например, оператор дипольного момента молекулы имеет вид:

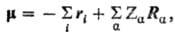
где r_i- радиус-вектор электрона i, R_α-радиус-вектор ядра а, Z_α- заряд ядра. При перестановке индексов тождеств. частиц оператор m не меняется. При инверсии m меняет знак; при поворотах каждый вектор r_i и R_a преобразуется одной и той же ортогональной матрицей, представляющей данный поворот, и т. д. Теория групп позволяет определить, будет ли среднее значение оператора или его недиагональный матричный элемент равен нулю, если известны лишь свойства симметрии этого оператора к волновых функций, входящих в выражения для ср. значения или в недиагональный матричный элемент. Такие утверждения приводят к т. наз. правилам отбора по симметрии. Например, квантовые переходы под влиянием монохроматич. излучения определяются матричным элементом дипольного момента перехода < Ф|m|Y >, равенство нулю которого означает нулевую вероятность перехода из состояния Y в состояние Ф, т. е. запрет на такой переход по симметрии. Спиновые функции для состояний разл. мультиплетности обладают разл. перестановочной симметрией, так что если оператор некоторой величины не зависит от спиновых переменных, то переходы, которые определяются воздействием, представляемым этим оператором, между состояниями разной мультиплетности запрещены. В фотоэлектронных процессах "встряхивания" вероятность переходов определяется межэлектронным взаимод. и пропорциональна квадрату модуля матричного элемента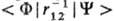; в ряде электромагн. процессов (напр., связанных с вращением плоскости поляризации светового луча) вероятность переходов определяется матричным элементом магн. момента системы и т. п.

Весьма существенны требования симметрии при построении разл. рода корреляц. диаграмм. Так, для двухатомных молекул при любом межъядерном расстоянии R и, следовательно, при любом его изменении С. м. сохраняется (группа C_,u или D_,u); это означает, что хотя электронная энергия разных состояний меняется при изменении R, отвечающая каждому из этих состояний волновая функция сохраняет свой тип симметрии. На корреляц. диаграмме "электронная энергия — межъядерное расстояние" линии электронной энергии, начинающиеся от предела "объединенный атом" и кончающиеся пределом "разъединенные атомы", отвечает обязательно состояниям одного и того же типа симметрии. К тому же линии, отвечающие состояниям одного типа симметрии, не пересекаются (правило непересечения).

Эти условия — сохранение типа симметрии и непересечение линий одной и той же симметрии — остаются справедливыми при некоторых дополнит. ограничениях и для орбитальных корреляц. диаграмм. Сохранение симметрии орбиталей важно учитывать при взаимодействии молекул, ведущих к хим. реакциям, если отдельные операции симметрии для системы взаимодействующих молекул сохраняются при всех расстояниях между молекулами. В этих задачах соблюдаются т. наз. правила сохранения орбитальной симметрии, налагающие определенные ограничения на возможные механизмы осуществления той или иной реакции (см. Вудворда — Хофмана правила).

Нарушения симметрия, как правило, бывают связаны с тем, что на ППЭ имеются эквивалентные области, переход между которыми затруднен. Это обстоятельство может проявляться по-разному. В качестве примера рассмотрим ППЭ, на которой имеются два эквивалентных минимума, разделенных достаточно высоким и широким барьером и отвечающих двум оптич. изомерам. Каждый из изомеров представляет собой нестационарную систему с очень большим временем жизни; стационарному состоянию системы отвечает равная вероятность нахождения в обеих потенц. ямах. Др. пример — появление таких нестационарных состояний при возбуждении. Например, при фотоионизации молекулы O₂ возникает состояние иона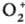, которое формально отвечает удалению на бесконечность электрона не с мол. орбиталей 1σ_g или 1σ_u, а с атомной 1s-орбитали; такие 1s-ионизованные состояния у обоих ядер нестационарны (как и в случае оптич. изомеров), однако минимумы на ППЭ разделены очень высоким потенц. барьером, что и ведет к появлению при ионизации O₂ несимметричного состояния-иона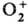. Наличие достаточно изолированных, но эквивалентных областей типа потенц. ям или ложбин приводит и к появлению локальных колебаний, также отвечающих нестационарным состояниям с большими временами жизни, что позволяет объяснить "несимметричную" диссоциацию, напр. H₂O → OH + Н.

^{Лит.: Хохштрассер Р., Молекулярные аспекты симметрии, пер. с англ., М., 1968; Каплан И.Г., Симметрия многоэлектронных систем, М., 1969; Болотин А. Б., Степанов Н.Ф., Теория групп и ее применение в квантовой механике молекул, М., 1973; Байкер Ф. Р., Симметрия молекул и молекулярная спектроскопия, пер. с англ., М., 1981; Фларри Р. Л., Группы симметрии. Теория и химические приложения, пер. с англ., М., 1983; Зоркий П.М., Симметрия молекул и кристаллических структур, М., 1986.}

_{Н. Ф. Степанов}