Степенная функция

Степенна́я функция

Функция f (x) = х^а, где а — фиксированное число (см. Степень). При действительных значениях основания х и показателя а обычно рассматривают лишь действительные значения С. ф. x^a. Они существуют, во всяком случае, для всех х > 0; если а — рациональное число с нечётным знаменателем, то они существуют также для всех х < 0; если же знаменатель рационального числа а чётный, либо если и иррационально, то x^a не имеет действительного значения ни при каком х < 0. При х = 0 степенная функция x^a равна нулю для всех а > 0 и не определена при а < 0; 0° определённого смысла не имеет. С. ф. (в области действительных значений) однозначна, за исключением тех случаев, когда а — рациональное число, изображаемое несократимой дробью с чётным знаменателем: в этих случаях она двузначна, причём её значения для одного и того же значения аргумента х > 0 равны по абсолютной величине, но противоположны по знаку. Обычно тогда рассматривается только неотрицательное, или арифметическое, значение С. ф. Для х > 0 С. ф. — возрастающая, если а > 0, и убывающая, если а < 0. С. ф. непрерывна и дифференцируема во всех точках её области определения, за исключением точки х = 0, в случае 0 < а < 1 (когда непрерывность сохраняется, но производная обращается в бесконечность); при этом (x^a)' = ax^a-1. Далее,

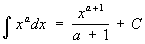
, при a ≠ -1;

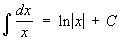
в любом интервале, содержащемся в области определения подынтегральной функции.

Функции вида у = cx^a, где с — постоянный коэффициент, играют важную роль в математике и её приложениях; при а = 1 эти функции выражают прямую пропорциональность (их графики — прямые, проходящие через начало координат, см. рис. 1), при а = —1 — обратную пропорциональность (графики — равносторонние гиперболы с центром в начале координат, имеющие оси координат своими асимптотами, см. рис. 2). Многие законы физики математически выражаются при помощи функций вида у = cx^a (см. рис. 3); например, у = cx² выражает закон равноускоренного или равнозамедленного движения (у — путь, х — время, 2c — ускорение; начальные путь и скорость равны нулю).

В комплексной области С. ф. z^a определяется для всех z ≠ 0 формулой:

, (*)

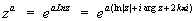
где k = 0, ± 1, ± 2,.... Если а — целое, то С. ф. z^a однозначна:

.

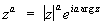
Если а — рациональное (а = p/q, где р и q взаимно просты), то С. ф. z^a принимает q различных значений:

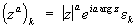
где ε_k = 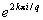— корни степени q из единицы: 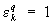и k = 0, 1, …, q — 1. Если а — иррациональное, то С. ф. z^a — бесконечнозначна: множитель ε^α2κπι принимает для разных k различные значения. При комплексных значениях а С. ф. z^a определяется той же формулой (*). Например,

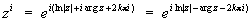
так что, в частности, 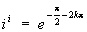, где k = 0, ± 1, ± 2,....

Под главным значением (z^a)₀ С. ф. понимается её значение при k = 0, если —π< argz ≤ π (или 0 ≤ argz < 2π). Так, (z^a)= |z^a|e^{ia arg z}, (i)₀=e ^-π/2 и т.д.

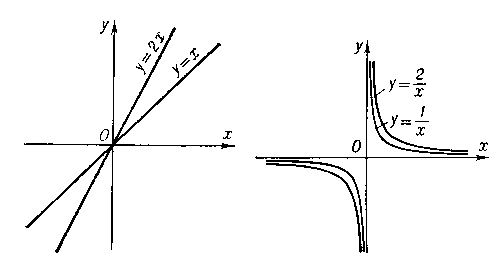
Рис. к ст. Степенная функция.

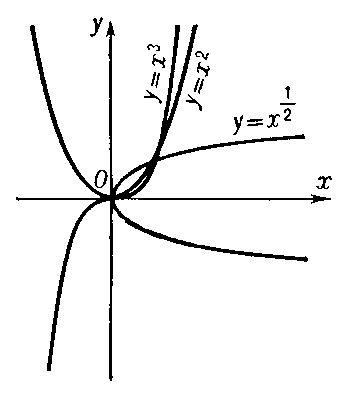
Рис. к ст. Степенная функция.